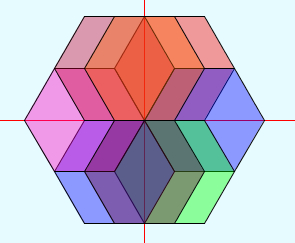
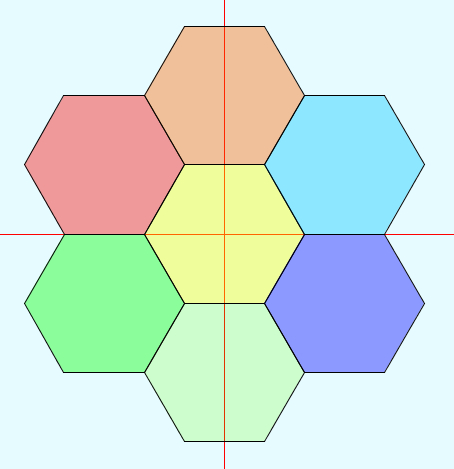
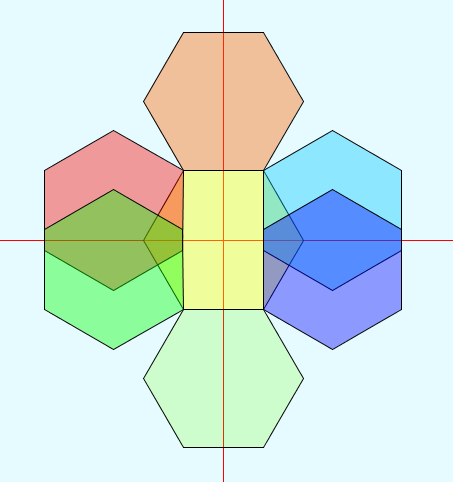
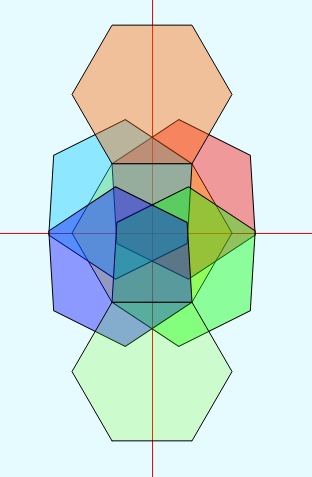
zeshoek "Vhoek

zeshoek "Vhoek_n6" bekijk de 4 roterende zeshoeken terug naar de inleiding naar het voorbeeld animatie met negen zeshoeken

De zeshoek bestaat uit 6 gelijkzijdige driehoeken met zijde n. ga naar de site met de formules

De binnenhoek is (6-2) * 180 / 6 = 120 graden. De zeshoek staat bij 30 graden rotatie op een hoekpunt.

De lijn van vlak naar vlak of diameter van de binnencirkel = 2*hn = 2*sqrt(3*n*n/4); = n*sqrt(3); (sqrt(3); wordt ook wel de theodorus constante genoemd)

De lijn van hoek naar hoek met twee tussenhoeken is de diameter van de buitencirkel = 2*n

 

class Vhoek_n6 extends Vormen { 
Vhoek_n6(float n_, int d_, float x_, float y_, float hoek_, color c1_) {  
 super();  
 n = n_;   
 x = x_;   
 y = y_;   
 hoek = hoek_;  
 c1 = c1_;  
 d = d_;  
 } 
void display() {  
 fill(c1);  
 // noStroke();  
 pushMatrix();  
 translate(x, y);  
 rotate(radians(hoek)); 
 float  hn = sqrt(3*n*n/4); 
 beginShape();  
 if (d == 0) {vertex(-n/2,hn);  vertex(-n,0);      vertex(-n/2,-hn);   
              vertex(n/2,-hn);  vertex(n,0);       vertex(n/2,hn);}   
 if (d == 1) {vertex(0,0);      vertex(-n/2,-hn);  vertex(0,-2*hn);   
              vertex(n,-2*hn);  vertex(3*n/2,-hn); vertex(n,0);}   
 if (d == 2) {vertex(n/2,hn);   vertex(0,0);       vertex(n/2,-hn);    
              vertex(3*n/2,-hn);vertex(2*n,0);     vertex(3*n/2,hn);}   
 if (d == 3) {vertex(0,2*hn);   vertex(-n/2,hn);   vertex(0,0);    
              vertex(n,0);      vertex(3*n/2,hn);  vertex(n,2*hn);}  
 if (d == 4) {vertex(-n,2*hn);  vertex(-3*n/2,hn); vertex(-n,0);    
              vertex(0,0);      vertex(n/2,hn);    vertex(0,2*hn);}  
 if (d == 5) {vertex(-3*n/2,hn);vertex(-2*n ,0);   vertex(-3*n/2,-hn);    
              vertex(-n/2,-hn); vertex(0,0);       vertex(-n/2,hn);}   
 if (d == 6) {vertex(-n,0);     vertex(-3*n/2,-hn);vertex(-n,-2*hn);    
              vertex(0,-2*hn);  vertex(n/2,-hn);   vertex(0,0);}  
 if (d == 7) {vertex(-n/2,0);   vertex(-n,-hn);    vertex(-n/2,-2*hn);    
              vertex(n/2,-2*hn);vertex(n,-hn);     vertex(n/2,0);}  
 if (d == 8) {vertex(-n/2,2*hn);vertex(-n,hn);     vertex(-n/2,0);    
              vertex(n/2,0);    vertex(n,hn);      vertex(n/2,2*hn);}   
 endShape(CLOSE);  
 popMatrix();  
 }  
}

schets met 4 roterende zeshoeken

bekijk de roterende zeshoeken

 

Vormen [] vorm; 
 
void setup() { 
  size(780, 560); 
 // fullScreen(); 
  float x = width/2; 
  float y = height/2; 
  float n = height/7; 
  float  hn = sqrt(3*n*n/4); 
  vorm = new Vormen[7]; 
  vorm[0] = new Vhoek_n6(n, 0, x, y, 0, color(255, 255, 0, 100)); 
  vorm[1] = new Vhoek_n6(n, 6, x-n/2, y-hn, 0, color(255, 0, 0, 100)); 
  vorm[2] = new Vhoek_n6(n, 1, x+n/2, y-hn, 0, color(0, 200, 255, 100)); 
  vorm[3] = new Vhoek_n6(n, 4, x-n/2, y+hn, 0, color(0, 255, 0, 100)); 
  vorm[4] = new Vhoek_n6(n, 3, x+n/2, y+hn, 0, color(0, 0, 255, 100)); 
  vorm[5] = new Vhoek_n6(n, 8, x, y+hn, 0, color(100, 255, 0, 50)); 
  vorm[6] = new Vhoek_n6(n, 7, x, y-hn, 0, color(255, 100, 0, 100)); 
} 
 
void draw() { 
  background(#E6FBFF); 
  //assenstelsel 
  stroke(255, 0, 0); 
  line (width/2, 0, width/2, height); 
  line(0, height/2, width, height/2); 
  stroke(0);  
   
  for (int i = 0; i < 7; i++) 
  { 
  vorm[i].display(); 
  } 
   
  vorm[1].dpRotLi(vorm[1]); 
  vorm[2].dpRotRe(vorm[2]); 
  vorm[3].dpRotRe(vorm[3]); 
  vorm[4].dpRotLi(vorm[4]);  
} 
 
void keyPressed() {        
   if (key == 's') {       
    noLoop();       
  }      
        
   if (key == 'r') {          
    loop();       
  }       
}

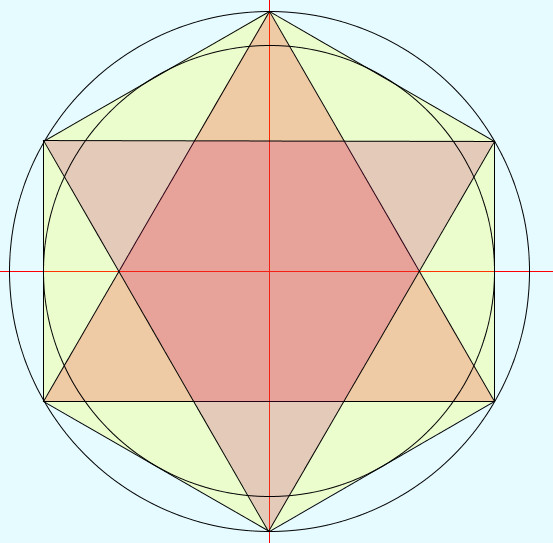
zeshoek ster

De schets maakt gebruik van objecten van de classes "Vhoek_n6" , "Drieh_nh" , "Ellips" en de superclass "Vormen"

 

Vormen vorm0; 
Vormen vorm1; 
Vormen vorm2; 
Vormen vorm3; 
Vormen vorm4; 
  
void setup() {  
  size(780, 780);  
  float x = width/2;  
  float y = height/2;  
  float n = height/3;  
  
  vorm0 = new Vhoek_n6(n, 0, x, y, 30,                       color(255, 255, 0, 50)); 
  vorm1 = new Drieh_nh(n*sqrt(3), 1.5*n, 6, x, y+n/2, 0,     color(255, 0, 0, 50));  
  vorm2 = new Drieh_nh(n*sqrt(3), 1.5*n, 6, x, y-n/2, 180,   color(200, 0, 100, 50)); 
  vorm3 = new Ellips  (n*sqrt(3)/2, n*sqrt(3)/2 ,0, x, y, 0, color(255, 0)); 
  vorm4 = new Ellips  (n, n ,0, x, y, 0,                     color(255, 0)); 
}  
  
void draw() {  
  background(#E6FBFF);  
  //assenstelsel  
  stroke(255, 0, 0);  
  line (width/2, 0, width/2, height);  
  line(0, height/2, width, height/2);  
  stroke(0);   
    
  vorm0.display(); 
  vorm1.display(); 
  vorm2.display(); 
  vorm3.display(); 
  vorm4.display(); 
}

Flevopink